Build your own planet
- Thread starter lizzienewell
- Start date
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
I've got an aspect of geometry which I'm puzzling over. This model is an icosahedron (20 equilateral triangles) projected on sphere with each face of the icosahedron subdivided into four triangles for 80 triangular faces. When I scaled up, the subdividing pieces came out too short. I have two overlapping layers and they didn't quite reach across the space, but the model still went together. The first model in is the background. The stringers hide the gaps left by parts being too short.
I built the model again and forced the subdividing pieces to reach across. Here is the result. Parts warped into pentagonal spirals. I like the effect, but in a few places the joints tore. The centers of the pentagons are higher than the interstitial un-warp triangles.

I thought that all 80 triangles would be identical. They're not. I don't quite understand why. I imagine the sphere as made up of 20 tetrahedrons with all 60 degree angles. Or another way to think is of twelve rays extending from the center with 60 degrees between each ray. Regardless of scale, any centered sphere will have the rays hitting it in the same places. When I subdivide each tetrahedron. I add rays with 30 degrees between rays. If these rays were projected on flat surfaces--the flat triangular top of a tetrahedron, all triangles would be the same size. When I project them onto a curved surface they aren't. The central triangle of each icosahedral face is larger. ??? but when people built geodesic domes all units are the same size. Aren't they? I'm probably treading over old ground.
I think I'll cover this model with thin white paper. With a light inside you'll be able to see the spirals but you won't see the torn joints. I seemed to have moved away from astronautics and space. Maybe this should be over in science fiction or with other. Still this structure is relevant to space architecture. A sphere and hemispherical domes have the lowest surface area and they're strong . Quiet suitable for things which have a lot of pressure on the inside or outside. It's good for enclosing an atmosphere. This is also the basic shape used for Dyson Spheres such as the one shown in the novel Hex by Alan Steele. Building a Dyson spheres doesn't make sense to me. A Dyson sphere is a sci-fi concept of enclosing an entire star in a sphere to utilize all the power put out by the star. The limitation is the strength of materials to build the sphere. Also in the novel Hex, this sphere spins to produce artificial gravity with no mention made about gravity only working at the equator. I haven't read Hex but I looked over reader reviews.
For my next build I'm going to allow the subdividing parts to become cylindrical. Sometime I'll get back to the initial goal of a model of a planet.
I built the model again and forced the subdividing pieces to reach across. Here is the result. Parts warped into pentagonal spirals. I like the effect, but in a few places the joints tore. The centers of the pentagons are higher than the interstitial un-warp triangles.

I thought that all 80 triangles would be identical. They're not. I don't quite understand why. I imagine the sphere as made up of 20 tetrahedrons with all 60 degree angles. Or another way to think is of twelve rays extending from the center with 60 degrees between each ray. Regardless of scale, any centered sphere will have the rays hitting it in the same places. When I subdivide each tetrahedron. I add rays with 30 degrees between rays. If these rays were projected on flat surfaces--the flat triangular top of a tetrahedron, all triangles would be the same size. When I project them onto a curved surface they aren't. The central triangle of each icosahedral face is larger. ??? but when people built geodesic domes all units are the same size. Aren't they? I'm probably treading over old ground.
I think I'll cover this model with thin white paper. With a light inside you'll be able to see the spirals but you won't see the torn joints. I seemed to have moved away from astronautics and space. Maybe this should be over in science fiction or with other. Still this structure is relevant to space architecture. A sphere and hemispherical domes have the lowest surface area and they're strong . Quiet suitable for things which have a lot of pressure on the inside or outside. It's good for enclosing an atmosphere. This is also the basic shape used for Dyson Spheres such as the one shown in the novel Hex by Alan Steele. Building a Dyson spheres doesn't make sense to me. A Dyson sphere is a sci-fi concept of enclosing an entire star in a sphere to utilize all the power put out by the star. The limitation is the strength of materials to build the sphere. Also in the novel Hex, this sphere spins to produce artificial gravity with no mention made about gravity only working at the equator. I haven't read Hex but I looked over reader reviews.
For my next build I'm going to allow the subdividing parts to become cylindrical. Sometime I'll get back to the initial goal of a model of a planet.
- Apr 5, 2013
- 13,499
- 9,551
- 228
It is accrued intolerance. Unless you are within at minimum +/- .005" of a inch, you will start having major problems. I would start with the polar triangles, as there will be fewer, and any adjustments can be more easily fixed, as you work your way to the equator, there are larger triangles, and the intolerance becomes easier to fix.
When I fix violins, this issue comes up all the times, as some luthiers think it is an art form, when it is an art form, and a craft. The art is in using the craft to get the best tone ut of the violin, the craft is in adjusting the height of the bridge to the style of the person playing. Someone who presses hard and goes through 3 bows per performance, i.e. Charlie Daniels, has to have a very high bridge and much space between the strings and the fret board.
It is also like skinning the hull of a ship. You start at the bow and stern, as the middle pieces are easier to fix, as their shapes are usually much more simple (not a strip planked, but modern hull).
If you put ink on the edges of the sphere, and rolled them on paper, you would have the exact shape, but this is the perimeter, and does not account for the compound curve. This, mathematically is Non-Euclidean geometry, where the angles of the triangles can never add up to 180 degrees.
p.s. In a Dyson sphere, the sphere itself would create a gravitational field, and it's size would probably create a situation of crushing gravity! Even asteroids have gravity, and some are very small, but are solid metals.
When I fix violins, this issue comes up all the times, as some luthiers think it is an art form, when it is an art form, and a craft. The art is in using the craft to get the best tone ut of the violin, the craft is in adjusting the height of the bridge to the style of the person playing. Someone who presses hard and goes through 3 bows per performance, i.e. Charlie Daniels, has to have a very high bridge and much space between the strings and the fret board.
It is also like skinning the hull of a ship. You start at the bow and stern, as the middle pieces are easier to fix, as their shapes are usually much more simple (not a strip planked, but modern hull).
If you put ink on the edges of the sphere, and rolled them on paper, you would have the exact shape, but this is the perimeter, and does not account for the compound curve. This, mathematically is Non-Euclidean geometry, where the angles of the triangles can never add up to 180 degrees.
p.s. In a Dyson sphere, the sphere itself would create a gravitational field, and it's size would probably create a situation of crushing gravity! Even asteroids have gravity, and some are very small, but are solid metals.
I've taken several different approaches. I built an icosahedral framework and then fit the four-triangle units inside each of the 20 triangular spaces. I put in the units across from each other and skipping triangular spaces so that I wouldn't get accrued intolerance. (one part pushing the next part over and that part pushed over even more with the last unit not fitting). Does that make sense? It's like tightening the lug nuts on a tire. The units are have 4 point slots for a lot of play so that they can be adjusted to fit the framework. Nearly every one of them ended up adjusted out as far as it would go.
 Here's the framework.
Here's the framework.
 And the subdividing unit going in. That triangle in the middle of the unit is coming out too small. I've been stretching them to fit.
And the subdividing unit going in. That triangle in the middle of the unit is coming out too small. I've been stretching them to fit.
 this is the subdividing unit in a smaller scale. Each section of the ring is the same size which is half the size of the struts in the icosahedral framework.
this is the subdividing unit in a smaller scale. Each section of the ring is the same size which is half the size of the struts in the icosahedral framework.
So as an experiment I removed the framework and forced the parts to fit the slotted cross pieces. I ended up with spirals with the parts too long, every one of them.
I guess I need to draw a picture. I put the units together first in pairs, connected pairs for quads then put together quads, ending up by putting together hemispheres.(three quads to two quads) Again trying to avoid accrued intolerance. Next time I might try 2 sets of 5 pairs together and then connect equal hemispheres. The nifty thing about tessellated shapes (made of repeated units) is that as long as you keep every unit the same you end up with something interesting.
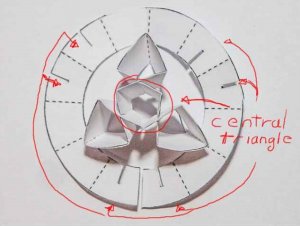 Each unit is made from an 8" circle (2 inch in this picture) each of the fold lines is at 30 degrees with the rotation point at the center of the circle. The central triangle slots together for a 2 layer thickness.
Each unit is made from an 8" circle (2 inch in this picture) each of the fold lines is at 30 degrees with the rotation point at the center of the circle. The central triangle slots together for a 2 layer thickness.
 If I try this again I'll put in only 3 folds so that the triangles will curve together, all gaps equal, no straining.
If I try this again I'll put in only 3 folds so that the triangles will curve together, all gaps equal, no straining.
 This is without the framework so that the units can take their natural shape.
This is without the framework so that the units can take their natural shape.
 Here's the framework.
Here's the framework. And the subdividing unit going in. That triangle in the middle of the unit is coming out too small. I've been stretching them to fit.
And the subdividing unit going in. That triangle in the middle of the unit is coming out too small. I've been stretching them to fit. this is the subdividing unit in a smaller scale. Each section of the ring is the same size which is half the size of the struts in the icosahedral framework.
this is the subdividing unit in a smaller scale. Each section of the ring is the same size which is half the size of the struts in the icosahedral framework.So as an experiment I removed the framework and forced the parts to fit the slotted cross pieces. I ended up with spirals with the parts too long, every one of them.
I guess I need to draw a picture. I put the units together first in pairs, connected pairs for quads then put together quads, ending up by putting together hemispheres.(three quads to two quads) Again trying to avoid accrued intolerance. Next time I might try 2 sets of 5 pairs together and then connect equal hemispheres. The nifty thing about tessellated shapes (made of repeated units) is that as long as you keep every unit the same you end up with something interesting.
 Each unit is made from an 8" circle (2 inch in this picture) each of the fold lines is at 30 degrees with the rotation point at the center of the circle. The central triangle slots together for a 2 layer thickness.
Each unit is made from an 8" circle (2 inch in this picture) each of the fold lines is at 30 degrees with the rotation point at the center of the circle. The central triangle slots together for a 2 layer thickness. If I try this again I'll put in only 3 folds so that the triangles will curve together, all gaps equal, no straining.
If I try this again I'll put in only 3 folds so that the triangles will curve together, all gaps equal, no straining. This is without the framework so that the units can take their natural shape.
This is without the framework so that the units can take their natural shape.- Apr 5, 2013
- 13,499
- 9,551
- 228
Folds are tricky to calculate. You would be better making each triangle separately, then checking them with a set of vernier calipers to make sure they are exact. If you made a mini "Brake" for folding , I have a 38* one for folding steel, you would get consistent results, Folding using the edge of a rule is not accurate enough. you must have two surfaces connected to each other to give one side the same fold, the cut the others to match. You'll eventually get it your way, but you'll be chasing your tale, and trying to produce these in any numbers will be laborious. You might try making a master jib, inside, or outside, your preference, that all triangles are shaped on. Then you can have a consistent series. Measuring these things with even plastic hobby verniers will show you how fast things go off. The fact that the sides can collapse is giving you a built in flaw, in which the off dimension gets passed down the line.
"but when people built geodesic domes all units are the same size. Aren't they?"
Actually the sides of the triangles are of different lengths when contructing a geodesic dome. There are some equilateral triangles and some isosceles triangles. Here is a website with a calculator used to figure the lengths of the triangle sides.
http://www.desertdomes.com/
The Dome Calculator uses the desired radius to figure the length of the triangle sides. The link to the Reverse Dome Calculator on the Dome Calculator page lets you input a length of one side and it calculates the length of the other sides and the radius of the dome.
The site is for those wishing to make a metal frame for geodesic domes but the information can be used to contruct cardboard domes. I have used the information to make cardboard triangle panels for some domes.
Here is a site with lots of polyhedra nets.
http://www.korthalsaltes.com/
Perhaps you could get some inspiration or ideas from there.
Actually the sides of the triangles are of different lengths when contructing a geodesic dome. There are some equilateral triangles and some isosceles triangles. Here is a website with a calculator used to figure the lengths of the triangle sides.
http://www.desertdomes.com/
The Dome Calculator uses the desired radius to figure the length of the triangle sides. The link to the Reverse Dome Calculator on the Dome Calculator page lets you input a length of one side and it calculates the length of the other sides and the radius of the dome.
The site is for those wishing to make a metal frame for geodesic domes but the information can be used to contruct cardboard domes. I have used the information to make cardboard triangle panels for some domes.
Here is a site with lots of polyhedra nets.
http://www.korthalsaltes.com/
Perhaps you could get some inspiration or ideas from there.
- Apr 5, 2013
- 13,499
- 9,551
- 228
Thanks SCEtoAUX
I wish Buckminster Fuller was a member, he'd have to be alive for that!!!
I wish Buckminster Fuller was a member, he'd have to be alive for that!!!
SCEtoAUX, That's just what I needed. I probably should have Googled geodesic domes before building but what fun would there be in that? Equilateral and iscosceles triangles are synonyms, but you're right not all the triangles are equilateral thus the gaps or spirals in my model. What the site calls strut A is longer than strut B. This wasn't noticeable until I scaled up. Given the way the struts are laid out as a circle, I can't easily make strut A longer than B. I think curving rather than folding the transition from B to A is the simplest solution. this will result in a small triangular gap at each joint between A and B. It will also require less scoring and so be simpler to construct. I'm aiming for the simplest possible construction.That's my game.
"but when people built geodesic domes all units are the same size. Aren't they?"
Actually the sides of the triangles are of different lengths when contructing a geodesic dome. There are some equilateral triangles and some isosceles triangles. Here is a website with a calculator used to figure the lengths of the triangle sides.
http://www.desertdomes.com/
- Apr 5, 2013
- 13,499
- 9,551
- 228
The more spherical you want the dome, the more different angles you will need. Equal size triangles will make a dome, (1V category), little rounder, Pentagram and Hexagon, but a nearly spherical will require many different shapes (6V category) , this will give you the most spherical construct though.
This link does it for you = http://www.ziptiedomes.com/geodesic-dome-calculators/geodesic-dome-calculator-index.htm
This link does it for you = http://www.ziptiedomes.com/geodesic-dome-calculators/geodesic-dome-calculator-index.htm
V2 seems the best for the purpose of providing solid support behind the surface of a spherical map. As the number of facets increases so does the production time and materials. The increase in roundness doesn't seem worth the increase in materials and time. I'm after designing the best process for building this model. This side trip into strut length has been great. I think I've just removed 8 steps per unit (6 folds gone) That's 120 steps removed. I was feeling frustrated by the strut length problem and couldn't quite make sense of it. It sure helps to have all of you to talk with. Thanks.
I changed design and rebuilt. To allow for the difference in size of struts I made some of the bends over a #5 knitting needle. This puts in a curve which gives enough allowance for the difference while still building the unit out of a circle. I'm pleased with the result. I think it looks like bone structure.
Here is the triangle unit ring folded and ready to assemble.

Use of the knitting needle.

The units in various stages. Notices the curved corners on the inner triangles.

Here are the curved parts in place. The corners at the center of the pentagons are flush. Those on the perimeter are curved with a gap. Here you can see how I marked the knitting needle bends with 12 pt dotted lines.


Here is the triangle unit ring folded and ready to assemble.

Use of the knitting needle.

The units in various stages. Notices the curved corners on the inner triangles.

Here are the curved parts in place. The corners at the center of the pentagons are flush. Those on the perimeter are curved with a gap. Here you can see how I marked the knitting needle bends with 12 pt dotted lines.


- Apr 5, 2013
- 13,499
- 9,551
- 228
Maybe you should make yourself a little "Brake", for bending sheets of thin metal and cardboard. I have a 38" one for metal fabrication, they look like this, very easy to make a tiny one... Every bend will be exactly the same.
I like this best, it could be made from wood. The two nuts press down on the sheet you are going to fold, or multiple sheets, and the picture explains the process best, the rest a variations on a theme.
Best
Best:
Explain theory
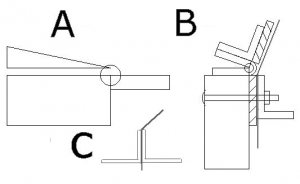
I like this best, it could be made from wood. The two nuts press down on the sheet you are going to fold, or multiple sheets, and the picture explains the process best, the rest a variations on a theme.
Best
Best:

Explain theory

That looks great for metal or heavy stock. My stuff is still enough small scale that I can make the folds quickly and accurately by hand. The cutting seems to be the most tedious part of the process
Maybe you should make yourself a little "Brake", for bending sheets of thin metal and cardboard. I have a 38" one for metal fabrication, they look like this, very easy to make a tiny one... Every bend will be exactly the same.
I like this best, it could be made from wood. The two nuts press down on the sheet you are going to fold, or multiple sheets, and the picture explains the process best, the rest a variations on a theme.
Best
Best: View attachment 149095
Explain theory
View attachment 149096
- Apr 5, 2013
- 13,499
- 9,551
- 228
You cannot replicate anything perfectly by hand. I wanted to show you the process. This is for accuracy, not the heaviness of the material. You can get to high quality Rulers, and make one of these by gluing Popsicle sticks, and using little plastic hinges, that sell for $2.95 for 6 at any hobby shop, ask for aileron hinges. You would then be able to produce perfect parts. Remember, we humans cannot repeat like the machines we design to do so. You will be astonished by how much time this saves, and for any other model, how perfect the bends are. The cutting is the most tedious parts, but when I look at your pictures, I see beds, no linear folds. 
Onward. I worked up to skinning the model and after trying some different approaches discovered the design needed more stingers. They ended up with a interesting sort of shape. Here is the structure before the new stringers.

And partly skinned. The little glowing hole is in the door to the access port. The plastic tab which acts as a light switch comes through the hole and acts as a latch.

Here's another view which shows the newly designed stringers on the left. On the right the light is shining through my different experiments with stringers and panels.

Here's with the room lights on. It seems I've designed a glowing soccer ball. It's more rigid than a soccer ball which makes is suitable for my purposes but it would break if you kicked it around a lot. I'm considering hooking it to a 24 hour clock so that it would rotate just Earth. It might have to be in a smaller size. I'm not sure how much weight a clock movement can handle. I also might do just the southern hemisphere.

And with the door to the access port opened. I put a coil of poster putty at each corner to hold the door closed. I might come up with a better solution. I also may consider reinforcing the hinge with fabric tape for mounting artwork. Right now it's a single layer of index paper. I could do a pintle hinge but the door doesn't need to be that durable. I'm going to start over because I want the new stingers under the old straight stringers(this will allow the skin to be flatter) and because I tried a number of different things with the skin panels.


And partly skinned. The little glowing hole is in the door to the access port. The plastic tab which acts as a light switch comes through the hole and acts as a latch.

Here's another view which shows the newly designed stringers on the left. On the right the light is shining through my different experiments with stringers and panels.

Here's with the room lights on. It seems I've designed a glowing soccer ball. It's more rigid than a soccer ball which makes is suitable for my purposes but it would break if you kicked it around a lot. I'm considering hooking it to a 24 hour clock so that it would rotate just Earth. It might have to be in a smaller size. I'm not sure how much weight a clock movement can handle. I also might do just the southern hemisphere.

And with the door to the access port opened. I put a coil of poster putty at each corner to hold the door closed. I might come up with a better solution. I also may consider reinforcing the hinge with fabric tape for mounting artwork. Right now it's a single layer of index paper. I could do a pintle hinge but the door doesn't need to be that durable. I'm going to start over because I want the new stingers under the old straight stringers(this will allow the skin to be flatter) and because I tried a number of different things with the skin panels.

I started over again. This time I'm production-lining the parts by scoring and cutting as a batch. I can fit six at once on my drafting table. Hey look a not yet assembled Metal Earth Star Wars model in the back peeking over the top of a sphere.

Here are the ten parts of the frame daisy chained together.

I love the shapes which appear as parts go together. This snowflake pattern will become a sphere like the ones in the background.


Here are the ten parts of the frame daisy chained together.

I love the shapes which appear as parts go together. This snowflake pattern will become a sphere like the ones in the background.

- Apr 5, 2013
- 13,499
- 9,551
- 228
Those look absolutely fantastic. The stringers, especially with the night lighting would make for some really cool spheres stuck on the side of a space station. In the daylight, it looks like you have reinvented the Wiffle Ball!! You have to go stiffen one of these up, and have some kid pitcher throw the living bejesus out of it, just to see what happens!! 
I've been thinking about the space station idea  I'm tempted to give one to some kids and have them throw it around. The PVA glue I'm using dries to a rubbery consistency. I think this flexibility would make it hold up fairly well.
I'm tempted to give one to some kids and have them throw it around. The PVA glue I'm using dries to a rubbery consistency. I think this flexibility would make it hold up fairly well.

